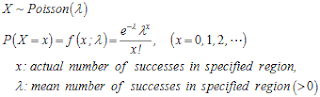My Statistics: 2011

2011년 7월 14일 목요일

My Android 개발팁 1 (in Menifest)

<application android:icon="@drawable/icon" android:label="@string/app_name">
     
        <activity android:name=".UnitMainActivity"
            android:theme="@android:style/Theme.NoTitleBar"
            
            android:screenOrientation="portrait"
            
            android:label="@string/app_name">
            <intent-filter>
                <action android:name="android.intent.action.MAIN" />
                <category android:name="android.intent.category.LAUNCHER" />
            </intent-filter>
        </activity>
        <activity android:name=".UnitActivity"
            android:theme="@android:style/Theme.NoTitleBar"
            android:screenOrientation="portrait"
            android:windowSoftInputMode="adjustResize"
            
            />
        <activity android:name=".ShowActivity"
                  android:theme="@android:style/Theme.Dialog"
                  android:screenOrientation="portrait">
        </activity>
    </application>

2011년 7월 13일 수요일

단위변환 제작기 (UnitConv Maker)

단위변환 제작기는 사용자가 원하는 형식으로 만들 수 있는 단위변환 툴입니다.
안드로이드용 모바일 앱으로 영어(UnitConv Maker)와 한글(단위변환 제작기)용이 있습니다.
UnitConv Maker (for English): Android Market에 등록되어 있습니다.
단위변환 제작기 (for Korean): T-Store에 등록되어 있습니다.

기본 17개에 대한 단위시스템이 주어져 있고, 사용자가 원하는 형식으로 수정이 가능합니다.
또한 사용자가 원하는 새로운 단위시스템을 100개까지 추가할 수 있습니다.

사용 예

새로운 단위시스템을 추가하고 사용해보는 예제입니다.

초기화면에서 추가로 들어가면 위와 같은 화면이 나오는데
예는 원화로 달러를 사고 팔 때를 예로 들어 만들어 본 것입니다.
US$ BUY 에는 달러를 살 때, 1US$ = 1,075won 이 필요하다는 의미입니다.
저장을 선택하면 초기화면(단위시스템 선택 화면)으로 돌아갑니다.

초기화면에서 Exchange Ratio를 선택하면 위의 화면이 나타나는데,

1,000US$를 사기 위해서 1백7만5천원이 필요하다는 것을 보여줍니다.

이와 같이 사용자가 원하는 다양한 종류의 단위시스템을 추가할 수 있어

실생활에 아주 유용한 도구로 생각이 됩니다.

2011년 7월 7일 목요일

돗수분포도 (Distribution Chart)

Average, Variance, Standard Deviation

모집단 (Population)

표본 (Sample)

일반적으로 통계분석을 행할 시, 모집단에서 표본을 추출하여 분석을 하기 때문에

여기에서는 특별한 표현이 없는 한, 표본에 대한 통계량으로 표현합니다.

Cp, CpK

단측규격 양측규격

돗수분포도 예제

전체파일 또는 LOT 별로 기초 통계치 및 분포도를 보여 줍니다.

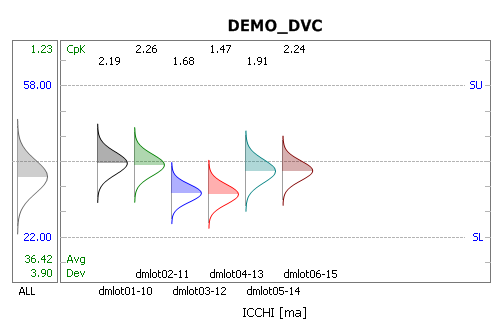
아래 차트는 ICCHI 항목의 전체 LOT에 대한 돗수분포도를 보여줍니다.

전체 6개 LOT의 451개의 데이터가 통계 계산에 적용되었고,

Avg: 36.42, STD: 3.90, CpK: 1.23으로 되어 있습니다.

아래 차트는 위 차트에서 스펙라인 오른편의 최상위 박스를 선택했을 경우로

전체 LOT에 대한 해당 LOT의 특성치 (괄호안)를 보여줍니다.

즉, 72개 데이터 적용, Avg:37.84, STD: 2.36, CpK: 2.24으로 되어 있습니다.

2011년 7월 6일 수요일

트렌드 차트 (Trend Chart)

각 항목에 대한 LOT 데이터의 분포 모양 및 추이를 확인할 수 있습니다.

개별 파일의 분포와 파일명, CpK 값을 보여 줍니다.

규격이 있으면, 규격을 기준으로

규격이 없으면, 전체 데이터에 대한 평균, 편차값을 기준으로 Y축을 정렬합니다.

왼쪽 프레임에는 선택된 항목에 대한 전체 데이터의 특성을 보여줍니다.

트렌드 차트 예제

ICCHI 항목에 LOT 별 분포와 그 특성치를 보여줍니다.

항목관련 차트 (Item Chart)

전체 항목을 한 차트에서 확인할 수 있습니다.

각 항목의 규격을 동일선상으로 일치 시켜서 문제되는 항목을 쉽게 볼 수 있습니다.

(규격이 있을 경우 규격을 기준선으로, 없을 경우 6σ를 기준선으로 Y축을 보여줍니다.)

또한 마우스를 이동시키며 원하는 항목을 찾을 수 있는데, 좌측 프레임에서 해당 항목에
대한 분포 및 특성치를 볼 수 있습니다.

차트에서 현재 분석중인 항목 과 찾고 있는 항목을 볼 수 있습니다.

항목관련 예제

아래 차트는 DEMO_DVC 제품의 전체 항목의 분포도를 보여줍니다.

현재 iih_WDCH 항목을 분석하고 있는 중이고,
마우스 이동으로 PIN54 항목 (산포가 크고, 스텍하한(SL) 을 벗어난 데이타가 많은)의
특성치를 왼쪽 프레임에서 볼 수 있습니다.

2011년 7월 5일 화요일

두 집단 비교도 (Compare Chart)

두그룹간 모평균 차이에 대한 추정과 검정

통합분산, 표준오차

두 모평균차에 대한 신뢰구간

두 모평균차에 대한 가설검정

두그룹간 모분산에 대한 추정과 검정

두 모분산 비율에 대한 신뢰구간

두 모분산 비율에 대한 가설검정

비교도 예제

두개의 그룹간 (예, 개선전/후 비교) 비교된 분포 차트 및 통계치를 볼 수 있습니다.

아래 차트는 DEMO_DVC 제품의 ICCHI 항목의 두그룹간 비교도를 보여줍니다.

두그룹간의 모평균의 차이는 99.9%(**)로 매우 유의(2 그룹의 평균은 서로 다르다) 하고

모분산의 차이는 85.2%로 유의하지 않음(2 그룹의 분산은 서로 다르지 않다)을 보이고,

또, 모평균차의 95% 신뢰구간은 6.95±0.518임을 보입니다.

2011년 7월 4일 월요일

상관관계도 (Correlation Chart)

상관계수와 단순회귀선

단순회귀선의 기울기에 대한 유의성 검정 (F test)

종속변수 Y의 기대값 (Expected Value) 에 대한 신뢰구간

종속변수 Y의 개별치 (Data) 에 대한 예측구간

상관관계도 예제

아래 차트는 두 항목 ICCHI vs. ICCLO 에 대한 상관관계도를 보이는데, 전체 6로트 449개의

데이터가 계산에 적용, 상관계수(r)가 0.888으로 매우 유의하고, 회귀식(Y = 1.13X + 8.22)도

**로 매우 유의함을 보여줌.

데이터 주변의 점선은 99% 신뢰수준에서의 Y축 평균값 및 데이터에 대한 신뢰구간을 표현

한 것이고, ICCLO 30[mA]에서의 ICCHI 항목의 예측값을 볼 수 있다.

2011년 7월 1일 금요일

와이블 분포 (Weibull Distribution)

이 분포는 종종 부품의 고장까지의 시간 혹은 수명 등과 같이 신뢰성과 수명시험 문제에

적용된다.

와이블 분포의 특성

모수인 척도모수(scale parameter)와 형상모수(shape parameter)에 따라 분포의 모양 변함.
특히, 형상모수가 1인 경우 지수 분포(exponential distribution),
형상모수가 2인 경우 라이레히 분포(Rayleigh distribution)가 된다.

와이블 분포의 용도

⊙ 부품의 수명 추정 분석
⊙ 신뢰성 공학에서 실패 분석
⊙ 산업 현장에서 어떤 제품의 제조에 걸리는 시간

확률밀도함수 (pdf: probability density function)

기대값과 분산 (expected value and variance)

와이블 분포 예제

* 어떤 제품의 수명시간 X가 형상모수 2.2, 척도모수 1,200 인 와이블 분포를 따른다고

할 때, 이 제품이 적어도 1,500 시간 이상 작동할 확률을 구하라.

> 척도모수 1200, 형상모수 2.2 인 와이블 분포로, 1,500 이상일 확률은 0.19518 이다.

F 분포 (F-distribution)

분산이 같은 두 정규모집단으로부터 크기 n1과 크기 n2의 확률표본을 반복하여 독립적으로

추출한 후 구한 두 표본분산의 비율들의 표본분포는 F분포를 따른다. F 확률변수는 다음과

같이 분자의 자유도 (n1-1)이고 분모의 자유도 (n2-1)인 F 분포를 따른다.

F 분포의 특성

⊙ 항상 양의 값을 가지며, 비대칭(오른쪽으로 긴 꼬리)적인 분포모양을 가진다.
⊙ 단일 분포가 아닌 모수인 분자의 자유도와 분모의 자유도에 따라 분포의 모양이
변하는데, 분자의 자유도와 분모의 자유도가 커질 수록 정규분포에 가까워진다.

F 분포의 용도

⊙ 두 모분산의 비교, 추정 및 검정
⊙ 분산분석 및 회귀분석

확률밀도함수 (pdf: probability density function)

기대값과 분산 (expected value and variance)

F 분포 예제

* F 분포에서 분자의 자유도가 6, 분모의 자유도가 10일 때, 확률이 0.1 일 때의 확률변수

값을 구하라.

> 자유도 6, 10 인 F 분포로, 확률이 0.1 이면 F 확률변수값은 2.46058 이다.

* 위의 예제를 양측꼬리로 F 확률변수값을 구하라.

> 자유도 6, 10 인 F 분포로, 확률이 0.1 이면 F 확률변수값은 0.24631 와 3.21717 이다.

카이제곱 분포 (Chi-square distribution)

정규분포를 따르는 모집단에서 크기가 n인 표본을 무작위로 반복하여 추출하였을 때,

각 표본에 대해 구한 표본분산들은 카이제곱 분포를 따른다. 카이제곱확률변수는

다음과 같이 자유도 (n-1)인 카이제곱 분포를 따른다.

카이제곱 분포의 특성

⊙ 항상 양의 값을 가지며, 비대칭(오른쪽으로 긴 꼬리)적인 분포모양을 가진다.
⊙ 단일 분포가 아닌 모수인 자유도에 따라 분포의 모양이 변하는데, 자유도가 커질 수록
정규분포에 가까워진다.

카이제곱 분포의 용도

⊙ 모분산에 대한 추정과 검정
⊙ 관측도수가 이론상의 분포 또는 형태를 얼마나 잘 따르는 지에 대한 검증
⊙ 여러 집단 사이의 독립성 검정 (한 특성이 다른 특성에 영향을 미치는 가에 대한 검정)

확률밀도함수 (pdf: probability density function)

기대값과 분산 (expected value and variance)

카이제곱 분포 예제

* 카이제곱 분포에서 자유도가 5일 때, 확률이 0.1 일 때의 확률변수값을 구하라.

> 자유도 5 인 카이제곱 분포로, 확률이 0.1 이면 카이제곱 확률변수값은 9.23635 이다.

* 카이제곱 분포에서 자유도가 3일 때, 확률변수값이 5 일 때의 확률을 구하라.

> 자유도 3 인 카이제곱 분포로, 카이제곱 확률변수값 5 이면 0.17180 이다.

t 분포 (Student's t-distribution)

모평균과 모표준편차를 모르는 정규모집단에서 표본크기가 작은 경우에 모평균에 대한

추정과 검정을 할 경우 t 통계량을 이용하는데, 정규모집단으로 부터 크기 n인 표본을

무작위로 추출했을 때 표본통계량 t 는 자유도 (n-1)인 t 분포를 따른다.

t 분포의 특성

⊙ 표준정규분포와 유사(평균 0 이고 좌우 대칭인 종모양)하지만 표본 표준편차를 사용
하기에 분산이 더 크다.
⊙ 단일 분포가 아닌 모수인 자유도에 따라 분포의 모양이 변하는데, 자유도가 커질 수록
Z분포에 가까워진다.

확률밀도함수 (pdf: probability density function)

기대값과 분산 (expected value and variance)

t 분포 예제

* t 분포에서 자유도가 10일 때, 확률이 0.05 일 때의 t 확률변수값을 구하라.

> 자유도 10 인 t 분포로, 확률이 0.05 이면 t 확률변수값은 1.81245 이다.

* 위의 예제를 양측꼬리로 t 확률변수값을 구하라.

> 자유도 10 인 t 분포로, 확률이 0.05 일 때 t 확률변수값은 -2.22814 와 2.22814 이다.

정규 분포 (Normal distribution)

각종 자연현상이나 사회현상의 실제 응용에 있어 폭 넓게 사용되는 것으로 연속확률변수를

나타내는 가장 중요한 확률분포이다.

정규 분포의 특징

⊙ 정규곡선은 종모양을 나타낸다.
⊙ 평균을 중심으로 좌우대칭을 이룬다. (평균=중앙치=최빈치)
⊙ 모수인 평균과 분산이 주어지면 정규분포를 나타낼 수 있다.
⊙ 아래와 같이 68-95-99 rule 을 따른다.

확률밀도함수 (pdf: probability density function)

표준정규분포 (standard normal distribution)

표준정규분포는 정규분포에서 정규확률변수의 평균이 0 이고, 표준편차가 1 인 특별한

경우로 모든 정규확률변수 X는 위의 Z scale를 통해 z-점수(z-score)로 변환할 수 있다.

정규 분포 예제

* A 고등학교 3학년 1반 남학생들의 신장이 평균 170cm, 표준편차 8cm인 정규분포를

따른다고 한다. 키가 160cm 이하인 학생들의 확률을 구하라.

> 평균 170cm, 표준편차 8cm 인 정규 분포로, 160cm 이하일 확률은 0.10565 이다.

* 평균이 200이고 표준편차 8인 제품의 규격이 185~215 일 때, 이 제품에 대한 양품률을

구하라.

> 평균 200, 표준편차 8인 표준정규 분포로 185~215 일 확률은 0.93921 이다.

연속형 확률분포 (Continuous Probability Distribution)

연속확률변수 (continuous random variable)

일정한 실수구간 내에서 연속적인 값을 취하는 확률변수이다.

예를 들면, 남한강에 새로운 다리를 세우기 위해 남한강의 수심을 측정한다고 하자.

남한강의 수심은 최저 수심에서 최고 수심 사이의 모든 값을 가지게 되므로 연속확률

변수이다.

연속확률분포 (continuous probability distribution)

연속확률분포(함수)는 모든 x값에 대하여 0 이상의 값을 가져야 하고 전체를 적분하면 1

이 되어야 한다.

확률밀도함수 (pdf: probability density function)

연속확률변수(continuous random variable) X가 어떤 구간 내에서 취할 수 있는 무수한 값

x들에 대해서 확률을 대응시키는 함수를 말한다. 연속확률변수의 경우에는 어떤 특정한

값에 대한 확률(=0)은 구할 수 없어 아래에 보이는 것처럼 구간(interval)에 속하는 넓이를

적분하여 확률을 구하게 된다.

기대값과 분산 (expected value and variance)

가장 많이 사용되는 다섯가지 연속형 확률분포에 대하여 분포의 형태 및 확률값을 쉽게 볼 수 있도록 하였습니다.

분포의 종류:

⊙ 정규분포 (Normal Distribution)

⊙ t 분포 (t-Distribution)

⊙ 카이스퀘어분포 (Chi-square Distribution)

⊙ F 분포 (F Distribution)

⊙ 와이블분포 (Weibull Distribution)

포아송 분포 (Poisson distribution)

시간, 면적 등 지정된 단위 구간에서 확률변수 X (단위 사상의 발생 횟수)가 나타내는 분포임.
⊙ 어느 특정지역에서 하루 동안 발생하는 교통사고 건 수.
⊙ 회사 교환대에 10분 동안 걸려오는 전화의 수.

포아송 확률변수의 조건

⊙ 구간마다 발생하는 사상은 서로 독립이다.
⊙ 사상의 발생 확률은 구간의 길이에 비례한다.
⊙ 아주 작은 구간에서 두 번 이상의 사상이 발생할 확률은 0 이다.

확률질량함수 (pmf: probability mass function)